From Basics to Bots: My Weekly AI Engineering Adventure - 3

Hi Pythonistas!

Last prost I explored how our computer to compare sentences, and today I’m diving into the math that powers so much of AI, graphics, and robotics: matrix multiplication and 2D transformations. If you’ve ever wondered how video games spin characters or photos resize smoothly, matrix math is the key!

What’s a Matrix?

Think of a matrix as a grid or table of numbers like a spreadsheet. Matrices help computers handle lots of numbers at once. Multiplying them applies transformations, mixes data, or feeds inputs through neural networks.

Matrix Multiplication: The Core Idea

Multiplying matrix A by B blends the rows of A with the columns of B to create a new matrix. This is how data or shapes get transformed.

Let’s Transform a Triangle!

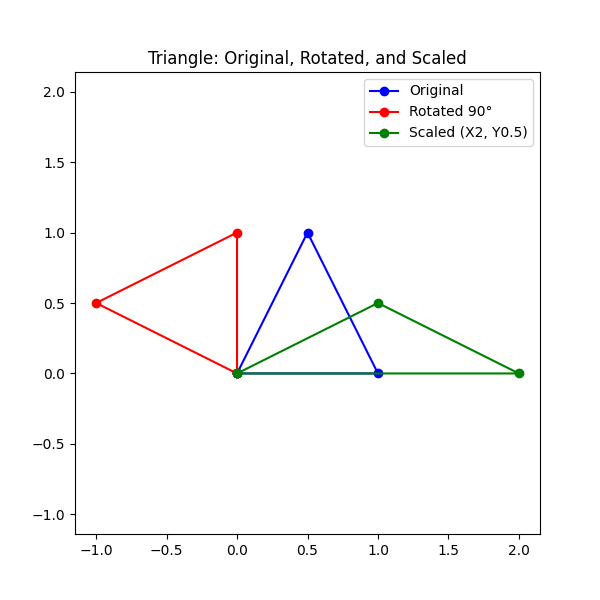
Step 1: Define a Triangle

import numpy as np

triangle = np.array([
    [0, 0],
    [1, 0],
    [0.5, 1]
])

Step 2: Rotation Matrix (Rotate 90°)

import math
angle = math.radians(90)
rotation = np.array([
    [math.cos(angle), -math.sin(angle)],
    [math.sin(angle),  math.cos(angle)]
])

Step 3: Scaling Matrix (Double Size on X, Half on Y)

scaling = np.array([
    [2.0, 0.0],
    [0.0, 0.5]
])

Step 4: Apply Transformations

rotated_triangle = triangle @ rotation.T
scaled_triangle = triangle @ scaling.T

Step 5: Visualize Original, Rotated, and Scaled Triangles

import matplotlib.pyplot as plt

def plot_shape(points, color, label):
    plt.plot(*zip(*(np.vstack([points, points[0]]))), color=color, marker='o', label=label)

plt.figure(figsize=(6,6))
plot_shape(triangle, 'blue', 'Original')
plot_shape(rotated_triangle, 'red', 'Rotated 90°')
plot_shape(scaled_triangle, 'green', 'Scaled (X2, Y0.5)')
plt.axis('equal')
plt.legend()
plt.title('Triangle: Original, Rotated, and Scaled')
plt.show()

Output

Practical Uses of These Transformations

• Computer Graphics & Games: Rotations, scalings, and translations make game characters move, spin, and grow.
• Machine Learning & Neural Networks: Data and weights multiply as matrices to train AI models efficiently.
• Image Processing: Resize or rotate photos, create data variations to improve AI training.
• Robotics & Engineering:  Robots calculate position changes and moves using these math tools.
• Data Science & Analytics: Transform and reduce data dimensions to spot patterns and simplify analysis.

What I Learned Today

• Matrix multiplication adjusts every point in a shape at once rotating or scaling the entire shape.
• These basic transformations are foundational to complex computer vision, AI, and graphics.

What’s Next?

In the upcoming post we will learn about norms and distance in vector