Hi Pythonistas!
Today we step into the fascinating world of probability. Probability tells us how likely something is to happen from rolling dice to making weather forecasts or building smart computers.
What’s Probability?
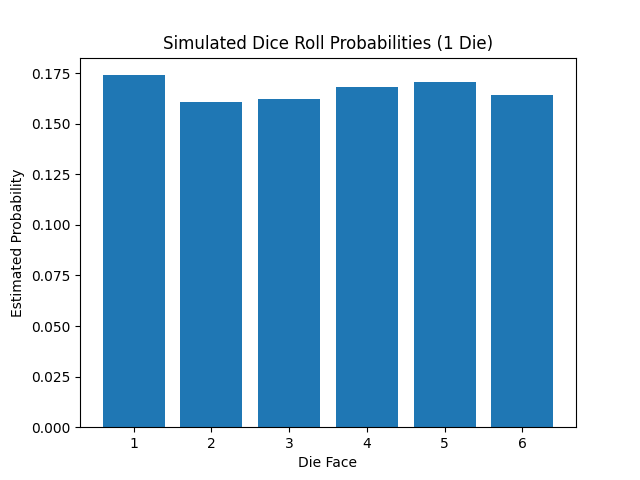
Probability is a number between 0 (impossible) and 1 (certain) that tells how likely something is. If you roll a standard 6 sided die, the chance of getting any particular face (like a 3) is 1/6≈0.166761≈0.1667. All possible outcomes together always add up to 1.
Simulating Dice Rolls in Python
Let’s roll a die lots of times and see if our results match the theoretical chances!
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
def roll_die(n_rolls):
return np.random.randint(1, 7, size=n_rolls)
n_rolls = 5000
results = roll_die(n_rolls)
# Count how many times we saw each face
counts = np.bincount(results)[1:] # Ignore zero index
probabilities = counts / n_rolls
print("Counts:", counts)
print("Probabilities:", probabilities)
# Plot the results
plt.bar(range(1,7), probabilities)
plt.xlabel('Die Face')
plt.ylabel('Estimated Probability')
plt.title('Simulated Dice Roll Probabilities (1 Die)')
plt.show()Output
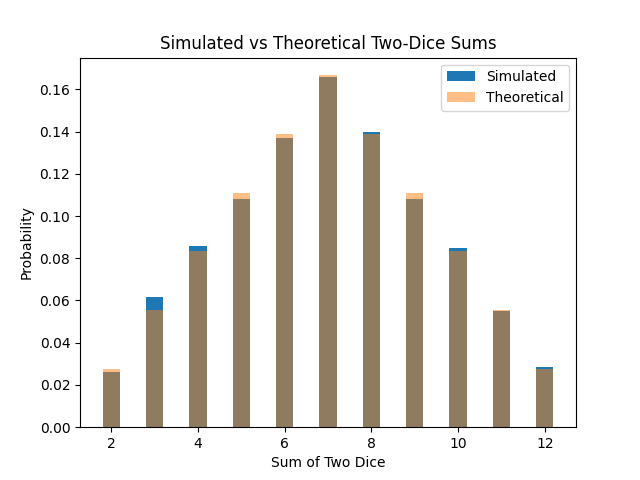
Rolling Two Dice: Some Sums Are More Likely
When you roll two dice, you add their faces. Some sums (like 7) happen more often than others, because there are more ways to get them.
def roll_two_dice(n_rolls):
die1 = np.random.randint(1, 7, n_rolls)
die2 = np.random.randint(1, 7, n_rolls)
return die1 + die2
n_rolls = 10000
results = roll_two_dice(n_rolls)
counts = np.bincount(results)[2:] # Sums start at 2
probabilities = counts / n_rolls
# Theoretical probabilities for sums 2 to 12
theoretical_probs = np.array([1,2,3,4,5,6,5,4,3,2,1]) / 36
plt.bar(range(2,13), probabilities, width=0.4, label='Simulated')
plt.bar(range(2,13), theoretical_probs, width=0.4, alpha=0.5, label='Theoretical')
plt.xlabel('Sum of Two Dice')
plt.ylabel('Probability')
plt.title('Simulated vs Theoretical Two-Dice Sums')
plt.legend()
plt.show()Output
Real-Life Applications of Probability
- Weather Forecasting: "70% chance of rain" is based on probability models.
- Games and Gambling: Board and casino games use probability to ensure fairness and determine odds.
- Business & Risk: Insurers and investors predict losses and gains using probability.
- Sports: Coaches use probability to plan strategies and maximize chances of winning.
- Machine Learning & AI: AI systems use probability to make smart predictions, from filtering spam to recommending a movie.
- Healthcare: Doctors use probability to evaluate treatment outcomes and risks.
- Everyday Decisions: We estimate chances in daily life like planning for traffic or deciding to bring an umbrella.
What I Learned
- Law of Large Numbers: The more you simulate, the closer your results match real-life probabilities.
- Combinations: Some results are more likely, simply because more outcomes lead to them (like getting a sum of 7 with two dice).
What’s Next
In the upcoming post we will learn about softmax and temperature scaling